Trick-Or-Treating With Rel

What's better than a bag full of candy for Halloween?

Here at RelationalAI, we're passing out knowledge graphs to trick-or-treaters this year. Come and get spooked with us as we solve a Halloween logic puzzle in Rel, our relational modeling language. You'll see how to model a problem, store facts, and infer new knowledge from those facts.

So grab your flashlight, put on your favorite costume, and let's go trick-or-treating with Rel!

The Setup

Four children --- two girls named Judy and Jessica, and two boys named Frank and Toby --- are going trick-or-treating. The children are all different ages, ranging from seven years old to 10 years old. Each child is accompanied by an adult: either their brother, sister, aunt, or uncle. They wear one of four costumes: a ghost, goblin, vampire, or werewolf. And each child carries a different color flashlight: red, blue, green, or orange.

We'll be given ten clues that we'll have to use to figure out how old each child is, what costume they wear, which flashlight they carry, and which adult accompanies them. But first, let's insert the base data we're working with into our database:

// write query

module trick_or_treat_data
    def adult = "Brother"; "Sister"; "Aunt"; "Uncle"
    def age = 7; 8; 9; 10
    def child = "Jessica"; "Judy"; "Frank"; "Toby"
    def costume = "Ghost"; "Goblin"; "Vampire"; "Werewolf"
    def flashlight = "Red"; "Blue"; "Green"; "Orange"
end

def insert:data = trick_or_treat_data

The trick_or_treat module has five member relations: adult, age, child, costume, and flashlight. Each relation is a set containing four values that are separated by semicolons. The adult, child, costume, and flashlight relations all contain strings, and the age relation contains integers.

The insert relation inserts the data from the trick_or_treat module into the database as a base relation named data. With the data inserted we can start to model the problem.

Let's create some entity and value types to represent the various concepts in the model:

// model

entity type Adult = String
entity type Child = String
entity type Costume = String
entity type Flashlight = String

value type Age = Int
value type Color = String
value type Name = String

You can use entity and value types to create instances of each type. For example, ^Child["Judy"] creates a Child instance representing the child named Judy. An entity instance is just a hash --- a unique ID that can be used to identify a specific entity.

Next, let's create entity relations that store instances of each entity in our model:

// model

def Adult = ^Adult[name] from name in data:adult
def Child = ^Child[name] from name in data:child
def Costume = ^Costume[name] from name in data:costume
def Flashlight = ^Flashlight[color] from color in data:flashlight

We'll also create a relation to store the four ages of each child:

// model

def Ages = ^Age[age] from age in data:age

Age is a property of a child. Normally, properties are assigned to entities using property edges --- relations containing tuples that pair an entity hash with a value type instance. In this case, however, defining Ages in a way that mimics an entity relation will help simplify our reasoning later on.

Speaking of property edges, let's go ahead and create some to assign properties to each of our entities:

// model

def has_name = (^Adult[name], ^Name[name]) from name in data:adult
def has_name = (^Child[name], ^Name[name]) from name in data:child
def has_name = (^Costume[name], ^Name[name]) from name in data:costume
def has_color = (^Flashlight[color], ^Color[color]) from color in data:flashlight

Finally, let's define operations on Age instances so that we can compare two Age instances and do some arithmetic with them:

// model

// 1
def age_int = transpose[^Age]

// 2
def minimum[x in Age, y in Age] = ^Age[minimum[age_int[x], age_int[y]]]
def maximum[x in Age, y in Age] = ^Age[maximum[age_int[x], age_int[y]]]

// 3
def (<)[x in Age, y in Age] = age_int[x] < age_int[y]
def (>)[x in Age, y in Age] = age_int[x] > age_int[y]
def (-)[x in Age, y in Int] = ^Age[age_int[x] - y]
def (+)[x in Age, y in Int] = ^Age[age_int[x] + y]

Here's a breakdown of what each numbered group of code does:

1. The ^Age relation maps integers to instances of the Age value type. So, ^Age[9] returns the Age instance (:Age, 9). The age_int relation inverts this map so that age_int[^Age[9]] returns the integer 9.
2. The built-in minimum and maximum relations can return the minimum and maximum of two integers, but don't know how to work with Age instances. These lines define the right behavior, so that the minimum of two Age instances is the one with the smaller corresponding integer value, and the maximum of two Age instances in the one with the larger integer value.
3. These lines define the < and > operators so that they can be used to compare two Age instances. The + and - operators are defined between Age instances and integers so that, for example, ^Age[7] + 1 returns ^Age[8].

Our setup is done. It's time to take a look at the clues.

The Clues

There are ten clues. Each clue expresses one or more fact about the childrens' relationships with adults, costumes, ages, and flashlights. We'll create two relations to store two kinds of facts:

1. The has relation holds facts of the form "X has Y."
2. The not_has relation holds facts of the form "X does not have Y."

For example, if the nine-year-old is wearing the ghost costume, then the has relation contains the tuple (^Age[9], ^Costume["Ghost"]). If the child accompanied by their sister does not carry the blue flashlight, then (^Adult["Sister"], ^Flashlight["Blue"]) is contained in has_not.

Clue One

Of the four children, there was the eight-year old, the child who dressed as a werewolf, the child who was accompanied by their sister, and the one who carried the red flashlight.

This clue tells us that the eight-year-old does not wear the werewolf costume, was not accompanied by their sister, and did not carry the red flashlight.

Similarly, the child wearing the werewolf costume is not eight years old, was not accompanied by their sister, and did not carry the red flashlight. And so on and so forth.

We can express this concisely in Rel:

// model

def clue1 = ^Age[8]; ^Costume["Werewolf"]; ^Adult["Sister"]; ^Flashlight["Red"]
def not_has(x in clue1, y in clue1) = x != y

This adds all pairs (x, y) of distinct elements of the clue1 set to the not_has relation.

Clue Two

Between the nine-year-old and Frank, who is older than Toby, one was dressed as a goblin and the other carried the green flashlight. First of all, clue two tells us that Frank is not nine years old.

// model

def not_has = (^Child["Frank"], ^Age[9])

You might look at the above line of code and think that that we've just overwritten the not_has relation. That is not the case. Relations in Rel are defined additively, so that the preceding definition adds the tuple (^Child["Frank"], ^Age[9]) to the existing not_has relation.

Clue two also tells us that Frank is older than Toby. In other words, Toby can't have any age that is greater than or equal to Frank's age.

//install

def not_has(child, age in Ages) {
    has(^Child["Frank"], age_frank)
    and age >= age_frank
    and child = ^Child["Toby"]
    from age_frank in Ages
}

Lastly, we can write "between the nine-year-old and Frank, one was dressed as a goblin and the other carried the green flashlight" as an if-then-else clause:

// model

def has {
    if has(^Age[9], ^Costume["Goblin"])
    then (^Child["Frank"], ^Flashlight["Green"])
    else if has(^Age[9], ^Flashlight["Green"])
         then (^Child["Frank"], ^Costume["Goblin"])
         else {}  // No tuple is added if neither if condition is true
         end
    end
}

Clue Three

Neither Frank nor Judy were accompanied by their sister while trick or treating. Judy did not carry an orange flashlight. Clue three tells us three facts that go in the not_has relation:

// model

def not_has {
    (^Child["Frank"], ^Adult["Sister"]);
    (^Child["Judy"], ^Adult["Sister"]);
    (^Child["Judy"], ^Flashlight["Orange"])
}

Clue Four

Toby's mother was upset that he cut up one of her favorite sheets to create his ghost costume.

Okay, so Toby wore the ghost costume:

// model

def has = (^Child["Toby"], ^Costume["Ghost"])

Clue Five

The child who dressed as a werewolf was accompanied by a male and did not carry a green flashlight. The child dressed as a werewolf must be accompanied by either their brother or their uncle.

So, if we know that a child wearing some costume other than the werewolf costume is accompanied by their brother, we know the child dressed as a werewolf must be accompanied by their uncle, and vice versa:

// model

def has {
    if has(costume, ^Adult["Brother"]), costume != ^Costume["Werewolf"]
    then (^Costume["Werewolf"], ^Adult["Uncle"])
    else if has(costume, ^Adult["Uncle"]), costume != ^Costume["Werewolf"]
         then (^Costume["Werewolf"], ^Adult["Brother"])
         else {}
         end
    end
    from costume in Costume
}

We also know that the child wearing the werewolf costume is not accompanied by their sister or their aunt, and doesn't carry the green flashlight:

// model
def not_has {
    (^Costume["Werewolf"], ^Adult["Aunt"]);
    (^Costume["Werewolf"], ^Adult["Sister"]);
    (^Costume["Werewolf"], ^Flashlight["Green"])
}

Clue Six

The nine-year-old was quite happy with her goblin costume, which she spent an entire week designing.

First, we know that the nine-year-old wore the gobline costume:

// model

def has = (^Age[9], ^Costume["Goblin"])

But we also know, since the nine-year-old is referred to as "her," that neither Frank nor Toby are nine years old:

// model

def not_has = (^Child["Frank"], ^Age[9]); (^Child["Toby"], ^Age[9])

Clue Seven

Either Frank or Toby carried a green flashlight. We can encode clue seven as an if-then-else clause. If Frank doesn't carry the green flashlight, then we know that Toby does, and vice versa:

// model

def has {
    if not_has(^Child["Frank"], ^Flashlight["Green"])
    then (^Child["Toby"], ^Flashlight["Green"])
    else if not_has(^Child["Toby"], ^Flashlight["Green"])
         then (^Child["Frank"], ^Flashlight["Green"])
         else {}
         end
    end
}

Clue Eight

The child who was accompanied by their brother was exactly two years older than the child who went with their sister.

If we know the age of the child accompanied by their sister, then we know the age of the child acompanied by their brother, and vice versa:

// model

def has {
    if has(age, ^Adult["Sister"])
    then (age + 2, ^Adult["Brother"])
    else {}
    end
    from age in Ages
}

def has {
    if has(age, ^Adult["Brother"])
    then (age - 2, ^Adult["Sister"])
    else {}
    end
    from age in Ages
}

We also know that the child who went with their brother must be at least two years older than the youngest child. In other words, their age can't be less than the minimum age plus two.

Similarly, the child who went with their sister can't be older than the maximum age minus two:

// model

def not_has = (age, ^Adult["Brother"]), age < min[Ages] + 2 from age in Ages
def not_has = (age, ^Adult["Sister"]), age > max[Ages] - 2 from age in Ages

Clue Nine

Jessica caught her uncle sneaking candy from her bag while they walked!

All right, then. Jessica was accompanied by her uncle:

// model

def has = (^Child["Jessica"], ^Adult["Uncle"])

Clue Ten

The child dressed as a ghost carried a blue flashlight.

Our last clue is another easy one. Let's add (^Costume["Ghost"], ^Flashlight["Blue"]) to the has relation:

// model

def has = (^Costume["Ghost"], ^Flashlight["Blue"])

Visualizing What We Know So Far

Now that we've encoded all of the clues, let's take a moment to see what we know so far.

We can do this by wrapping our has and not_has relations into two knowledge graphs.

The nodes of each graph are the Child, Ages, Costume, Adult, and Flashlight entity relations, and the edges of each graph are the has and not_has relations, respectively:

// model

def show(e, string) {
    (Child(e) or Adult(e) or Costume(e)) and has_name(e, ^Name[string])
    or Flashlight(e) and has_color(e, ^Color[string])
    or Age(e) and string = "%(age_int[e])"
}

def Things = Adult; Ages; Child; Costume; Flashlight

module HasKG
    def node = show[x] from x in Things
    def edge = (show[x], show[y]), has(x, y) from x, y
end

module NotHasKG
    def node = show[x] from x in Things
    def edge = (show[x], show[y]), not_has(x, y) from x, y
end

The show relation maps entity hashes and value type instances to string representations. Children, adults, and costumes are mapped to their name. Flashlights are mapped to their color. Ages are mapped to a string containing their integer value. The Things relation is the union of the Adult, Ages, Child, Costume, and Flashlight relations, expressed in Rel using the semicolon.

The nodes in each knowledge graph are the string representations of each thing in Things. In the HasKG, each edge is pair of strings representing pairs from the has relation. The HasNotKG pairs representations of pairs from the not_has relation.

We can visualize these knowledge graphs using the graphviz library, which is included with Rel:

// read query

def output = graphviz[HasKG]

Here's what the HasKG graph looks like:

We don't know much about who has what. But we can tell, for example, that since Toby has the ghost costume and the ghost cosutme has the blue flashlight, then Toby has the blue flashlight.

In general, the has relation should be transitive. That is, if (x, y) is in has and (y, z) is in has, then (x, z) should also be in has. Right now, the has relation, as we've defined it, is not transitive.

We'll fix that in a moment, but first let's take a look at the NotHasKG graph:

// read query

def output = graphviz[NotHasKG]

Here's what it looks like:

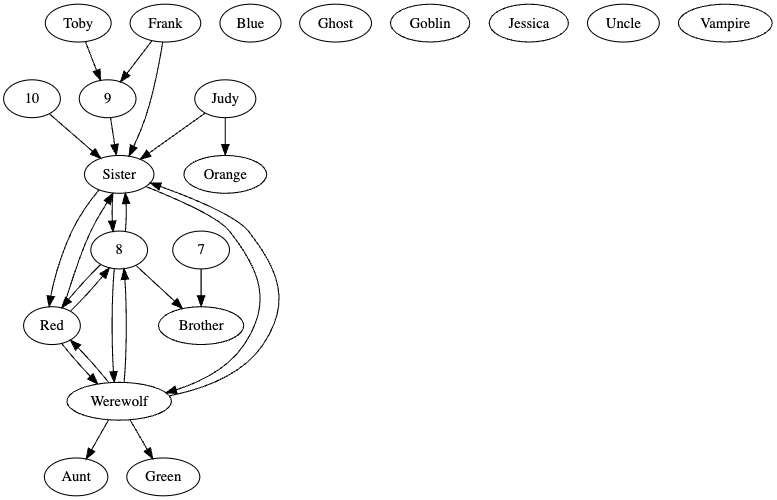
We know a lot more about what things don't have. Some of the edges are symmetric --- that is, for some values of x and y, both (x, y) and (y, x) are in not_has. In fact, the entire not_has relation should be symmetric since, if x does not have y, the y also does not have x.

The has relation should be symmetric as well. Let's build on what we've modeled so far and solve the puzzle.

Inferring the Solution to the Puzzle

First, let's make sure has is symmetric and transitive:

// model

def has = transpose[has]  // make sure has is symmetric
def has = has.has  // make sure has is transitive

The transpose relation swaps the order of the pairs in has. So if (x, y) is in has, then (y, x) is in transpose[has].

The second line uses the dot join operator to calculate the transitive closure of has.

// read query

def output = graphviz[HasKG]

Here's what the HasKG looks like after installing the preceding Rel code:

The not_has relation is also symmetric, but it isn't transitive since if x does not have y and y does not have z, we can't conclude that x does not have z.

However, there is a transitive dependence on the has relation. In other words, if x has y and y does not have z, then x does not have z. Similarly, if x does not have y, and y has z, then x does not have z.

Let's encode that in Rel:

// model

def not_has = transpose[not_has]
def not_has(x, y) = has.not_has(x, y), x != y
def not_has(x, y) = not_has.has(x, y), x != y

We have to make sure that x != y. If (x, x) were in not_has, it would mean that x does not have itself. It would be like saying that the child dressed as a ghost was not dressed as a ghost.

// read query

def output = graphviz[NotHasKG]

Here's what the NotHasKG looks like after updating not_has:

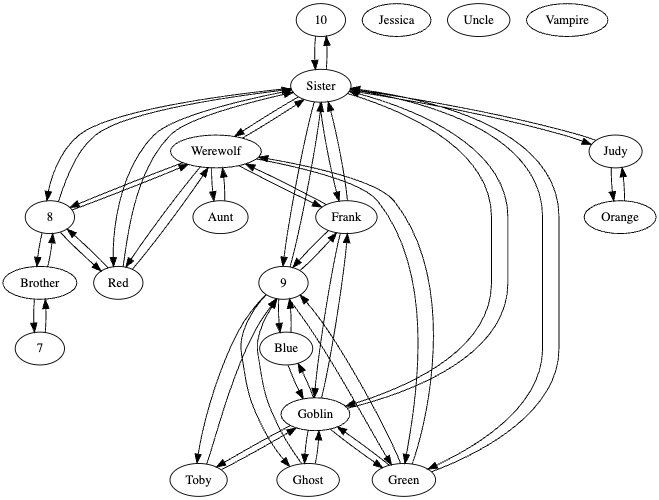
We're starting to get a bunch of new facts!

Next, we can infer more edges that should be in not_has from what we know is in the has relation. If x has y, then x does not have z for every z != y of the same type as y.

In other words, if Toby wears the ghost costume, the we know Toby doesn't wear the goblin, vampire, and werewolf costumes.

Here's how to model that in Rel:

// model

@inline
def infer_not_has[Type](x, z) {
    has(x, y)
    and Type(z)
    and Type(y)
    and z != y
    from y
}

def not_has = infer_not_has[Adult]
def not_has = infer_not_has[Ages]
def not_has = infer_not_has[Child]
def not_has = infer_not_has[Costume]
def not_has = infer_not_has[Flashlight]

The infer_not_has relation is a higher-order relation. It takes another relation as input, represented by the Type parameter. Higher-order relations are marked with the @inline annotation.

We can also infer edges that should be in the has relation based off what we know is in the not_has relation. If x does not have three things of the same type, then it must have whatever the fourth thing of that type is.

Here's what that looks like in Rel:

// model

// Helper relation that selects not_has pairs based on the
// type of the second element
@inline
def not_has_type[Type](x, y) = not_has(x, y) and Type(y)

@inline
def infer_has[Type](x, y) {
    count[not_has_type[Type, x]] = 3
    and y = diff[Type, not_has_type[Type, x]]
    and x != y
}

def has = infer_has[Adult]
def has = infer_has[Ages]
def has = infer_has[Child]
def has = infer_has[Costume]
def has = infer_has[Flashlight]

First, we create a not_has_type relation that selects pairs from not_has that have the same type in the second element of each pair. The infer_has relation counts the number of things of some Type that are related to x, and returns the tuple (x, y) where y is the remaining Type instance that x does not have.

These two relations, infer_not_has and infer_has are enough for Rel to compute the entire solution.

You can see that by visualizing the HasKG knowledge graph again:

// read query

def output = graphviz[HasKG]

It now looks like this:

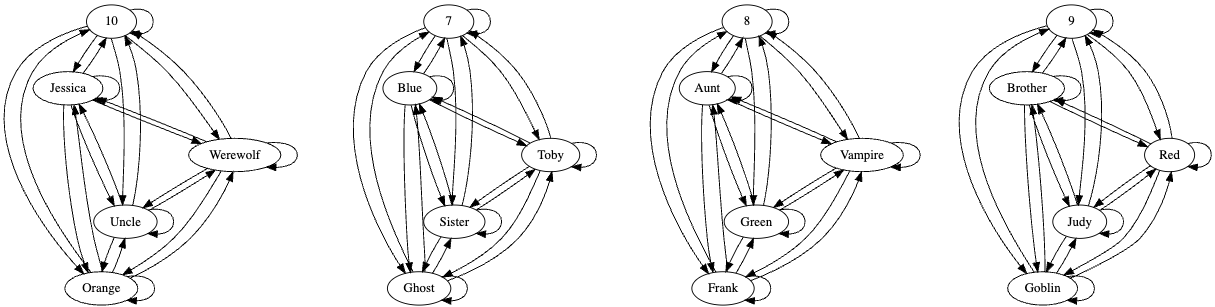
The HasKG graph has four cliques --- i.e., subgraphs containing every possible edge. Each clique represents the complete solution for each child.

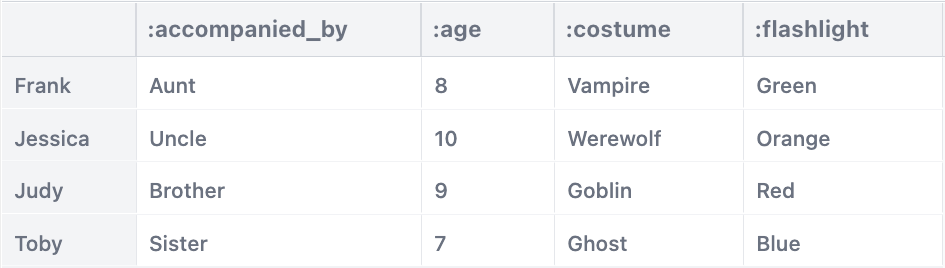
We can also display this solution as a table:

// read query

@inline
def show_solution(Type, name, solution) {
    has(child, e)
    and Child(child)
    and Type(e)
    and name = show[child]
    and solution = show[e]
    from child, e
}

def solution:costume = show_solution[Costume]
def solution:flashlight = show_solution[Flashlight]
def solution:age = show_solution[Age]
def solution:accompanied_by = show_solution[Adult]

def output = table[solution]

Here's what that looks like:

This little logic puzzle shows off a number of interesting features of Rel and RelationalAI's Relational Knowledge Graph System.

You saw how to:

• Model entites and entity properties using entity and value types.
• Define custom operators that work on value types.
• Model facts as tuples in relations.
• Create and visualize knowledge graphs.
• Infer new facts by computing symmetric and transitive closures and encoding logic.

That's a pretty tasty treat, if you ask me!